(김경환 교수님의 자료와 수업을 통해 제작되었습니다.)
4.3 Parzen Windows
4.2장에서 언급한 세 조건을 만족시키기 위해 부피를 줄이는 방법을 택하게 된다.

각 변의 길이를 $h_n$으로 하고, d는 demension의 수로 하여, hypercube의 부피를 정의한다.
다음은 window function이다.
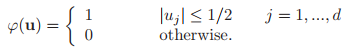
어떠한 샘플이 hypercube내에 있으면 1을 갖는 함수를 정의했다. 영역 밖에 있으면 0을 갖는다.
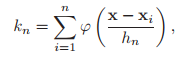
영역 안에 들어온 샘플의 수를 세기 위해, 시그마를 이용하여 $k_n$을 구해준 것이다.

폭 $h_n$에 대한 영향도 고려해주어야 하므로, delta함수를 정의한다. 이는 dirac delta function과 비슷한 역할을 하게 된다. x를 결정하는 R의 범위가 크다면, 우리가 선택한 x에 대한 신뢰성이 줄어들 것이고, 조금 더 space-averaged된 값을 얻게 될 것이다. R의 영역이 커질수록 smooth하고, $\delta_n(x)$가 줄어들게 되어, 피크 값이 낮아지는 경향성을 보이게 될 것이다. 피크 값이 날카로워 진다는 것은 추정에 대한 resolution이 높아진다는 것을 의미한다.


dirac-delta function과 같이, $h_n$에 관계 없이 부피가 1이 될 것이다. 이에 따라 $h_n$이 작아질 수록 피크 값이 커지는 것이다.

이 그림 역시 $h_n$이 커질수록 resolution이 낮은 smooth한 곡선을 얻게 되고, $h_n$이 작아질 수록 resolution이 높은 것을 볼 수 있다. $h_n$이 무작정 작아지는 것 만이 좋은 것이 아님을 볼 수 있는 데, 3장에서 봤듯이, 오히려 $h_n=1$일 때 전체적인 그림을 확인할 수 있다. $V_n$이 너무 작으면 추정의 통계적 변화성이 커지게 되는 것이다. 앞서 설명했던 3장의 overfitting과 비슷한 개념으로 이해할 수 있을 것이다. resolution이 너무 커서 샘플 데이터에 대해서만 맞게 되는 상황이 일어날 수 있는 것이다.
하지만, $n->\infty$의 상황은 다르다. 우리는 무한히 많은 샘플 수를 얻는다면, $p_n(x)$가 $p(x)$에 수렴한다고 말한다. 또한 분산은 0으로 수렴할 것이다.


다음은 수렴성을 보장하는 조건들이다.

다음과 같은 p(x)가 단변량 normal 분포를 갖는 경우 , 윈도우 함수도 같은 형태라고 생각하여 살펴보자.
또한, $h_n=h_1/\sqrt{n}$이다. $h_1$은 임의로 처리할 수 있는 파라미터이다.


위의 결과들은 n과 $h_1$에 따라 그래프 개형이 달라진다. n이 작아질수록 실제 개형과 달라지는 것을 확인할 수 있었고, 특히 n=1일 때에는 하나의 점, 샘플만 가지고 개형을 그려야 하는 것을 볼 수 있다. n=1에 대해서 살펴보면 $h_1$에 따라 뾰족한 정도가 다름을 알 수 있는데, 이는 $h_1$이 점을 담당하는 영역에 해당하기 때문이다.
$h_1$이 작아지면, 각각의 샘플에 대한 분포의 변화성이 커지게 되고, $h_1$이 클 때보다 더 많은 n을 필요로 하게 된다. 차원이 커질수록 샘플 수가 더 많이 필요한 점과 같다. 또, n이 무한대로 갈 때는 $h_1$에 상관없이 같은 분포, true분포에 도달함을 알 수 있다.

위 그림은 2차원에서의 비슷한 결과를 보여준다.

위 그림은 분포를 바꿔 $n, h_1$에 따라 똑같이 진행해 준 것이다. 위와 비슷한 결과를 얻을 수 있는 것을 볼 수 있다.

왼쪽은 h가 작은 경우, 오른쪽은 h가 큰 경우를 보인다. h가 작은 경우에는 점이 포함되는 영역이 작게 되므로 위 데이터에 대한 정확성은 높아질 수 있다. 하지만, overfitting과 같이 다른 샘플이 들어왔을 때 틀릴 가능성이 높아진다. 차원이 높아질수록 그보다 지수적으로 더 많은 샘플 수를 요구하게 되므로, 샘플 수가 부족하여 생기는 오류가 발생한다. 따라서, 적당한 h를 고르는 것이 필요할 것이다.
[Parzen Widows 장점]
> unimodal normal case와 bimodal mixture case가 모두 같은 접근 방법이 사용된다.
> 분포에 대한 가정이 필요없다.
> 샘플 수가 충분하면, 복잡한 타겟 밀도에 대한 수렴이 보장된다.
[한계점]
> 분포를 모르는 상태이므로, 매우 많은 샘플이 필요하다.
> curse of dimensionality
$V_1,V_2,\cdots,$에서 $V_n=V_1/\sqrt{n}$을 취한다고 하면, 유한한 n에 대한 결과들은 초기 부피에 대해 민감하게 작동할 것이다.
$V_1$이 매우 작다면, 샘플이 무한히 많지 않은 이상 대부분 비어있을 가능성이 높다.
$V_1$가 매우 크다면, 큰 cell 부피에 대해 평균내어 계산하므로, 민감한 반응을 못하고, 공간에 대한 해상도가 떨어진다.
이에 따라, 9장에서 general methods, including cross-validation에 대해 다룬다.
또한, 4.4장에서 $k_n$-Nearest-Neighbor Estimaion을 적용해볼 수 있다.
Reference
- pattern classification by richard o. duda
'Review > Pattern Classification' 카테고리의 다른 글
| [패턴인식]Chapter 4.5~6 The Nearest-Neighbor Rule (0) | 2022.10.18 |
|---|---|
| [패턴인식]Chapter 4.4 k_n-Nearest-Neighbor Estimation (0) | 2022.10.18 |
| [패턴인식]Chapter 4.1~2 Nonparametric techniques (0) | 2022.10.13 |
| [패턴인식]Chapter 3. Bayesian decision theory (2) | 2022.10.03 |
| [패턴인식]Chapter 2. Bayesian decision theory (0) | 2022.09.27 |



