(김경환 교수님의 자료와 수업을 통해 제작되었습니다.)
3.1 Introduction
우리는 2장에서 prior와 class-conditional densities를 알 때 최적의 classfier를 설계할 수 있는 방법에 대해 배워 보았다.
하지만, 실제로 이러한 확률적인 구조에 대해 정확하게 알기는 어려울 것이다. 상황에 대한 이해가 완벽하게 되지 않을 수 있고, 디자인 샘플과 트레이닝 데이터의 수가 제한되어 있기 때문.
이 문제를 해결하기 위해 접근할 수 있는 방법은, probablities와 densites를 추정하고, 그 값이 true values라고 생각하여 사용하는 것이다.
> prior를 추정하는것보다, class-conditional densities를 추정하는 것이 어렵다.
> 샘플 수는 너무 적고, feature vector x의 차원이 큰 것이 문제가 된다. 파라미터 수를 미리 알고, 문제에 대한 지식을 통해 class-conditional densities를 파라미터로 나타낼 수 있다면, 추정이 조금 더 쉬워질 것이다.
파라미터를 추정하는 문제는 통계학에서는 고전적인 문제라고 하며, 두가지 방법이 있다.
1. Maximum-likelihood estimation
> 파라미터가 고정되어 있지만 알려지지 않은 상태라고 간주한다.
> 값들 중, 실제 관측한 결과를 통해 얻은 probability가 최대화 되도록 하는 값을 정한다.
2. Bayesian estimation
> 파라미터를 알려진 prior distribution을 가진 random variables라고 간주한다.
> 샘플들을 관측함으로써 posterier density로 convert할 수 있다. 그럼으로써 우리가 추정하는 파라미터 값을 조정하게 된다.
> 샘플들을 추가적으로 관측하는 것은 posteriori density function을 뾰족하게 만드는 효과가 있다. 그럼으로써 파라미터들의 true 값 근처에서 피크를 만든다. 이를 Bayesian learning이라고 한다.
3.2 Maximum likelihood estimation
> 샘플 수가 증가할 수록 수렴성이 좋아진다.
> 다른 방법들보다 간단하다.
우선, 데이터들의 집합을 $D_1,\cdots,D_c$라 하자. 클래스에 따라 샘플들을 분리했기 때문에, c개의 데이터 집합으로 나온 것이다. (c : 클래스의 개수)
$D_j$의 샘플들은 확률 법칙 $p(x|\omega_j)$에 따라 독립적으로 뽑혀 졌다. 이러한 샘플들을 i.i.d(independent and identically distrbuted), 독립적이며 동일하게 분포하는 랜덤 변수들이다.
class-conditional densites의 form은 parameter vector $\theta_j$에 의해 정해진다고 하자.
class-conditional densites가 $N(\mu_j,\sum_j)$의 form을 갖는다 하면, $\theta_j$는 $\mu_j$와 $\sum_j$의 성분을 갖는다.
우리는 $\theta_j$ vector를 추정하기 위해 training sample에 대한 정보를 사용할 것이다.
문제를 간단히 하기 위해 samples $D_i$는 $\theta_j$에 대한 어떠한 정보도 주지 않는다고 가정하자. $(i\neq j) $즉, 클래스 간의 파라미터는 독립적이라고 가정하는 것이다. 이렇게 하면 각 클래스를 분리해서 다룰 수 있게 되며, $p(x|\theta)$로 부터 독립적으로 뽑은 훈련 샘플들의 집합 D를 사용해 unknown parameter vector $\theta$를 추정한다.
집합 D가 n개의 샘플 $x_1, \cdots, x_n$을 포함한다고 하자. 이 샘플들이 독립적으로 뽑혔기 때문에 다음과 같이 쓸 수 있다.


좌항은 샘플 집합에 대한 likelihood of $\theta$라고 한다.
여기서, $\theta$는 분포에 대한 form 정보를 담고 있는데, 샘플에 대한 분포를 가장 잘 표현하는 $\theta$를 $\hat{\theta}$를 정의하자. 즉, $p(D|\theta)$를 최대로 하는 $\theta$에 대한 maximum-likelihood이다.

맨 위 그래프는 데이터를 수집함에 따라, 분포가 여러개로 추정될 수 있는 부분을 의미한다. 점선이 그 추정된 4개의 분포이다. 두 번째 그래프는 likelihood를 $\theta$에 대한 함수로 그린 것이다. 데이터가 많아질 수록 실제 데이터의 분포의 정보를 가진 $\theta$가 하나로 추려질 것이고, 그에 따라 그래프가 특정 $\hat{\theta}$에서 뾰족해질 것이다.
마지막 그래프는 두번째 그래프를 로그를 취해주는 것이다. 로그의 특성은 2장에서도 언급했지만, 증가함수이기 때문에 로그를 취하더라도 대소관계가 변하지 않는다. 이 경우에도 함수값이 가장 큰 $\theta$를 정하면 그 값이 $\hat{\theta}$값이 된다. 이 $l(\theta)$를 log-likelihood라고 하며, $l(\theta)\equiv lnp(D|{\theta})$라 정의한다.
$\theta=(\theta_1,\cdots,\theta_p)^t $ 라고 정의하자. p개의 form에 대한 추정 vector $\theta$가 있는 것이다.
MLE의 방법대로, likelihood를 최대로 하고자, log-likelihood를 최대로 하는 $\theta$를 찾는다. 전개하면 다음과 같다.

1번째 식은 MLE의 정의이고, 두번째 식은 $D={x_1,\cdots,x_n}$이기 때문이다. 세번째 식은 $\theta$에 대한 gradient를 찾은 뒤, 이 값을 0으로 만드는 값을 찾아 그 값을 $\hat{\theta}$라고 하게 될 것이다. 즉, 다음 식과 같이 표현한다.

하지만, 이 값은 global maximum임을 보장할 수 없고, local minimum에 대한 정보도 포함하고 있다. 그 값을 비교하는 과정이 필요할 것이다.
지금까지는 MLE에 대한 정의, MLE를 전개하기 위해 필요한 정의들을 알아보았다. 이제 실제로 어떻게 수식적으로 적용될 수 있는지에 대한 부분을 살펴보자.
[The Gaussian case : Unknown $\mu$]


첫번째 식은 가우시안 확률(3번째 식)을 대입한 것이다. 두번째 식은 이 값을 $\theta$에 대한 gradient를 구해준 것이다. $\theta$는 $\mu$에 대한 정보만 알면 되므로, $\mu$에 대한 gradient를 구해주었다.

따라서, 이 그래디언트 값을 0으로 만들어, minimum값을 찾고자 한다. 위 파란색 식에서도 나왔지만, $l(\theta)$를 최소로 하는 $\theta$를 구하는 것이 목적이기 때문에, 왼쪽과 같은 식을 쓸 수 있다. 구한 결과, $\mu$는 위와 같다.
우리는 MLE를 사용해 $\mu$를 모르는 상태에서, 가장 분포의 form을 잘 표현할 수 있는 $\mu$를 찾았다. 그런데 결국, 우리가 일반적인 가우시안 분포에서 사용하는 평균 구하는 방식과 같은 결과를 얻을 수 있었다. arithmetic average를 구하는 것이다. 즉, sample mean이 가장 분포를 잘 표현하는 $\mu$가 되는 것이다. 흥미로운 결론이라 할 수 있을 것이다.
[The Gaussian case: Unknown $\mu$ and $\sum$]
평균과 분산을 모르는 경우에 대해 알아보자. $\theta_1=\mu, \theta_2=\sigma^2$이라 하자.

가우시안 확률에 대해 $\theta_1$과 $\theta_2$로 표현한 뒤, gradient를 구해주었다.
$\theta$는 평균과 분산으로 이루어진 벡터이기 때문에, gradient 역시 평균과 분산에 대해 각각 gradient를 구해주어야 한다. 행렬에서 1행에 있는 항은 $\theta_1$에 대한 그래디언트, 2행에 있는 항은 $\theta_2$에 대한 그래디언트이다.

여기에서도 흥미로운 결과를 얻을 수 있었다.
우리는 표본을 가우시안 분포라고 가정하고, 이 분포를 가장 잘 표현할 수 있는 $\theta$에 대해 알아보고자 한 것이다.
그 결과, 평균과 분산이 원래 가우시안 분포에서 구하는 방식과 같은 결과를 얻게 되는 것이다. 어느정도는 자연스러운 결과라고 할 수 있을 것이다. 변수가 여러개인 상황에서는 $x_k$역시 벡터가 되어야 할 것이다. 다음과 같이 구한다.

3.3 Bayesian estimation
MLE에서는 $\theta$를 고정시킨 뒤, 추정하는 과정을 거쳤다. Bayesian estimation에서는 $\theta$가 random variable이고, 트레이닝 시켜야 할 데이터라고 간주하고 과정을 진행한다. 얻은 데이터를 통해 posterior probability density를 구하는 것이 목적이다. ($P(\omega_i|x,D)$)

위 식은 posterior probability density를 구하기 위해, class-conditional density와 priori probability를 이용할 수 있다는 것이다. 이는 트레이닝 샘플들을 통해 얻을 수 있고, prior probabilites의 참값이 알려져 있거나, 간단한 계산에 의해 얻을 수 있다고 가정하고, $P(\omega_i)=P(\omega_i|D)$로 대체한다.
Bayesian estimation에서도 독립성에 대해 가정을 하게 된다. $D_i$안에 있는 샘플들은 $p(x|\omega_j,D)$에 영향을 주지 않는다. ($i\neq j$) 이를 가정하면 다음과 같은 식을 쓸 수 있게 되고, 간단한 계산이 가능해진다.
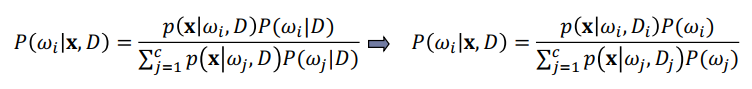
[The parameter Distribution]
> p(x)는 unknown 상태이지만, 알려진 parametric form(가우시안 form 등)이라 가정하자. 모르는 값은 $\theta$뿐이다.
> $p(x|\theta)$는 $\theta$가 알게 되거나 정해지면 완전하게 알 수 있다.
> 샘플을 관찰하기 전의 정보는 $p(\theta)$에 포함된다. 샘플들을 통해 posterior $p(\theta|D)$의 정보를 알 수 있게될 것이며, MLE에서처럼 그래프 모양이 $\theta$에 대해 뾰족해 질 것이다.
> 이제는 $\theta$에 대해 알고 싶은게 목적이 된다. 즉, 우리는 $p(x|D)$에 대해 알아내기 위해 $p(\theta|D)$를 찾는 것이 목적이 되었다는 것이다. $\theta$는 우리가 알고 있지 않은 성분이라는 것이고, 이 문제는 unsupervised learning이 된다. 우리가 알고 있는 form들로 나타내서 $\theta$에 대한 정보를 알고자 하는 것이 목적이다.


첫 번째 식은 MLE와 Bayesian estimation의 차이를 보여준다. bayesian learning method는 $\theta$를 random variable로 생각하여 문제를 풀어주는 것이다. 따라서 $p(x|D)$는 $\theta$에 영향을 받게 된다. 이에 데이터셋 D중에서, x를 구할 확률은 데이터셋 D중, x에 영향을 주는 모든 $\theta$에 대해 적분해준 값이 될 것이다. 이에 첫 번째 식이 나오게 될 것이다. 이에 MLE는 Bayesian estimatoion중, $p(\theta)$가 일정한 special case라 생각할 수도 있을 것이다.
두번째 식을 얻기 위해서는 우선 두 가지 식에 대해 알아야 한다.
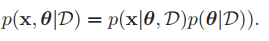

식 (3)의 증명을 하고자 Bayes rule에 대해 다시 공부해보았다. 아래 사이트가 도움을 주었다.
https://www.wikiwand.com/en/Bayes%27_theorem
Wikiwand - Bayes' theorem
Probability based on prior knowledge
www.wikiwand.com

식 (4)는 x를 선택하는 것과, 트레이닝 샘플 D를 선택하는 것은 독립적이다. 즉, x를 선택하는 것은 D에 영향을 받지 않는다. 따라서 식(4)가 성립한다. 식(3)과 (4)를 식(1)에 대입하면 식(2)를 얻게 된다.

이 식은 $p(x|D)$를 구하기 위해서는 $\theta|D)$를 구해야 한다는 것을 의미하며, $\theta$에 대한 정보를 알고 싶은 상황이다. 여기서 $p(theta|D)$는 unknown parameter vector이고, 만약 피크 값이 매우 뾰족하게 그려진다면, 우리는 $p(x|D)$를 $p(x|\hat{theta})$로 근사하여 쓸 수 있을 것이다. 즉, 우리가 구한 $\theta$가 신뢰할 수 있는 범위에 있다면 그 $\theta$를 신뢰하고, x의 분포로 나타내는데 쓰일 수 있다는 점을 의미한다.
또, 이 값이 만약 위와는 반대로 평평한 그래프라면, 즉 모든 분포의 가능성이 비슷하다면, (예를 들어 A 분포의 form을 띌 확률과 B 분포의 form...을 띌 확률이 비슷하다면) $p(x|\theta)$의 평균으로 구하게 될 것이다.
3.4 Bayesian Parameter Estimation: Gaussian Case
[The Univariate Case: $p(\mu|D)$]
$\mu$만 unknown parameter로 작용하고, univariate한 케이스에 대해 살펴보자.

우리는 위에서 $\theta$에 대해 추정할 때, random variables라 가정하고, $\theta$에 대한 추정을 확률적으로 접근한다고 했다. 따라서, 우리가 $\mu$에 대해 사전 지식이 어떠한 것이든, $\mu$를 $p(\mu)$에 대해 표현할 수 있음을 가정하자.

위에서 말하고자 하는 내용은 $\mu$의 추정이 확률적으로 일어나게 될 것인데, 그 분포를 나타내면 정규 분포의 형태를 띈다고 가정하는 것이다. 평균이 $\mu_0$라는 것은 $\mu$를 가장 잘 나타낼 수 있는 평균이 $\mu_0$라는 것이고, 아래의 식들에서 얻을 수 있는 추측 전에, 이전에 먼저 $\mu$에 대한 추측을 진행한 값이다.
$\sigma_0^2$은 $\mu$의 추정에 대한 불확실성이라고 볼 수 있을 것이다. $\sigma_0^2$이 작을수록 $\mu$의 추정을 $\mu_0$로 하는데 큰 무리가 없음을 뜻하는 것과 같을 것이다. 여기서 $\mu$의 분포가 gaussian 분포를 띈다는 것은 수학적으로 간단하게 하기 위함이다. $\mu$를 알고 있는 상태라는 것보다, 이 가정이 더 큰 가정은 아니기 때문에, 사용한다.

이 식은 $x_1,\cdots,x_n$이 각각 independent하게 뽑혔다고 가정하고, Bayes 공식을 사용한 것이다. 여기서 $\alpha$는 D에는 종속되나 $\mu$와는 독립적인 정규화 계수이다. 위 식에서 분모에 해당할 것이다. $p(D|\mu)$의 항은 MLE에서 썼던 식과 같은 식을 사용하여 $\Pi$의 형태로 나타나게 된다.
이는 training sample에 대해서 우리가 추정하려는 $\mu$가 어떻게 구해지는지에 대해 알아보고자 하는 것이다.
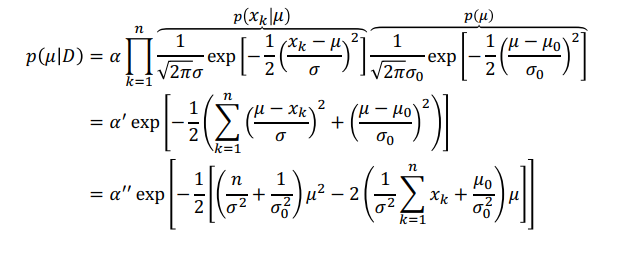
위 식은 $p(x_k|\mu) ~ N(\mu,\sigma^2)$과, $p(\mu) ~ N(\mu_0 ,\sigma_0^2)$임을 이용하였다.
가우시안끼리는 곱해도 가우시안 분포가 나오는 것을 확인할 수 있었고, 이에 $\mu$에 대한 2차식, quadratic function임을 알 수 있다. $\alpha,\alpha',\alpha''$는 $\mu$에 independent한 항들을 모아놓은 것이다.
위 식은 샘플 수 n에 상관없이 성립하기 때문에, $p(\mu|D)$는 가우시안 형태를 유지하게 된다. 그리고 $p(\mu|D)$는 reproducing density라 하고, $p(\mu)$는 conjugate prior라 한다. 가우시안 형태로 다음과 같이 쓸 수 있다.


이 식들은 $p(\mu|D)$를 얻기 위한 prior 정보가 어떻게 샘플들의 경험적인 정보와 연관되어 있는지를 보여준다. 대략적으로 말하자면, $\mu_n$과 $\sigma_n^2$은 n개의 샘플들을 통해 얻을 수 있는 참값 $\mu, \sigma^2$에 대한 가장 좋은 추측이라는 것이다. MLE에서의 n개의 데이터를 통해 얻은 피크값과 비슷한 개념이라 생각하면 될 것이다.
위에서도 언급했지만, $\mu_0$와 $\sigma_0$는 사전에 추측한 값 중 가장 좋은 값이다.
위 식에서 재밌게 볼 수 있는 부분은 (1)n이 무한대로 다가갈때, (2)$\sigma_0$가 0일 때, (3)$sigma_0$가 $sigma$보다 매우 클 때이다.
(1) n이 무한대로 다가갈 때
$\mu_n$의 식은 n이 커지면 $\mu_n$에 대한 계수가 1이 되는 것을 알 수 있다. 이는 $\hat{\mu_n}$과 $\mu_n$이 같아진다는 결론을 얻을 수 있고, $sigma$를 보면, n이 커짐에 따라 $\sigma/n$이 되는 것을 알 수 있다. n이 커짐에 따라 0에 접근하며, 이는 $\mu$에 대한 불확실성이 사라진다는 것이다. 이에 p(\mu|D)$는 피크 값이 날카로워지며, Dirac 델타 함수에 접근하는 것을 알 수 있는데, 이를 Bayesian Learning이라 한다.
또, $\hat{\mu_n}$과 $\mu_n$이 같아진다는 결론은, MLE에서도 얻을 수 있던 결과로 샘플 데이터가 많아지면 우리가 가우시안 form에서 원래 구했던 방식으로 $\mu$를 구하면 된다는 결론을 얻을 수 있는 것이다.
(2) $\sigma_0 = 0 $일 때
책에서는 $\mu_n$이 $\hat{mu_n}$과 $\mu_0$의 linear combination, 선형결합이라고 말하며 두 값 사이에 어딘가에 위치한다고 말한다. $\sigma_0$이 0이면 $\mu_n$은 $\mu$가 되는데, 이는 해석해보면 $sigma_0$이 0이라는 말은 처음에 추측했던 $\mu_0$가 맞을 확률이 굉장히 높다는 것을 말한다. 따라서 n에 관계없이 처음 예상했던 $\mu_0$로 고정된다는 것이다.
(3) $sigma_0$가 $sigma$보다 매우 클 때
이 말을 해석적으로 보자면, 처음에 추측한 $\mu$의 값에 대해 굉장히 확신이 없는 것이다. (2)번 케이스와 반대라고 생각하면 될 것 같다. 수식적으로 보면, $mu_n$은 $\hat{\mu_n}$에 가까워진다. 이 말은 처음 예측했던 $mu_0$가 신뢰성이 낮기 때문에, 샘플데이터로 얻을 수 있는 값으로만 $mu_n$을 추정하겠다는 것이다.
여기서( (2)와 (3) ) 사용한 개념, 선형결합에 대한 부분은 $\mu_n$은 $\hat{\mu_n}$과 $\mu_n$의 선형결합, 사전적인 추정과 샘플에 의한 추정으로 정해진다는 것 이었는데, 이는 $\sigma^2$과 $\sigma_0^2$의 비에 의해 결정된다고 볼 수 있다. 이를 dogmatism이라 한다.

[The Univariate Case: $p(x|D)$]
위에서는 $\mu$만 unknown parameter로 작용하고, univariate한 케이스에 대해 살펴보았고, $p(\mu|D)$를 얻었다. 이제, $\theta$에 대한 정보는 알게 되었으므로, 궁극적으로 얻고자 하는 class-conditional density $p(x|D)$에 대해 알아보자.

위 식에서 알 수 있듯이, $p(x|D) ~ N(\mu_n , \sigma^2+\sigma_n^2)$이다. 즉, $p(x|D)$의 분산은 true distribution에 대한 $\sigma^2$과 샘플데이터 n개로 얻을 수 있는 $\mu$에 대한 불확실성 $\sigma_n^2$을 더한 결과가 된다는 것이다.
예를 들어, 앞에서 $\mu$에 대한 추정이 확실하게 되어, $\sigma_n^2$이 0에 가까워 진다면, p(x|D)는 데이터가 있던 true distribution에 가까워 진다는 것을 말한다. 즉, p(x|D)의 분산이 $\sigma^2$과 같아진다는 말과 같다.
[The Multivariate Case]

Multivariate case인 경우에도 똑같이 증명해낼 수 있다.
3.5 Bayesian Parameter Estimation: General Theory
위에서는 Bayesian Parameter Estimation에서 density의 form이 가우시안 분포를 갖는다고 가정하고 문제를 풀었다. 이에 $\theta$가 다른 조건이라면 적용할 수 있겠느냐에 대한 부분이다.
우선, Bayes estimation은 다음과 같은 가정을 통해 구해졌다.
> $p(\omega_i|x)$를 구하기 위한 p(x|D)를 표현할 수 있는 $\theta$가 알려진 parametric form이지만, 그 중에 어떤 것을 선택해야 되는지는 모르는, unknown상태라는 것을 가정.
> $\theta$에 대한 사전 지식은 $p(\theta)$에 포함.
> $\theta$에 대한 정보는 n개의 샘플이 독립적으로 뽑힌 D에 포함되는 것을 가정.


2장에서 우리의 목표는 $p(\omega_i|x)$를 구하는 것이 목적이라고 했다.
> 식(1)을 통해 그 목적이 p(x|D)를 구하는 것으로 변경되었다. (3장)
> 식(2)를 통해 그 목적이 $p(\theta|D)$를 구하는 것으로 변경되었다.
> 식(3)을 통해 $p(\theta|D)$는 샘플들로 부터 얻을 수 있는 $p(D|\theta)$와 $p(\theta)$로 표현될 수 있다.
이에, form이 가우시안이 아니더라도, 위와 같은 방법으로 전개하면 p(x|D)를 구할 수 있을 것이다.

앞에서의 계산은 복잡하다. 조금 더 간단한 연산을 위해 recursive한 해법을 제공한다. 위 식에서 두번째 식을 이용하여 샘플 하나가 추가될 때, 이전 까지의 추정된 것과 곱하여 추정을 완성해 나가는 과정이다. 자주 쓰는 기법이라고 한다.
[Bayes estimation 정리]
Bayes estimation을 정리해보자면, 처음의 가정은 $p(\omega_i|x)$를 구하기 위한 p(x|D)를 표현할 수 있는 $\theta$가 알려진 parametric form이지만, 그 중에 어떤 것을 선택해야 되는지는 모르는, unknown상태라는 것을 가정하여 시작했다. 결국 목적은 $p(\theta|D)$를 구하는 것이 되었고, 이를 위해 $\theta$에 대한 사전 지식은 $p(\theta)$에 포함되고, $\theta$에 대한 정보는 n개의 샘플이 독립적으로 뽑힌 D에 포함되는 것을 가정했다. 이에 우리는 그 분포 p(x|D)가 우리가 가정했던 $\theta$의 분포와 얼마나 다른 결과를 얻는지를 수식적으로 전개하여 얻었다. n을 무한히 키우면 MLE와 같은 결과를 얻을 수도 있었다.
[Bayes method vs MLE]
1) Computational complexity
Bayes method는 complex mutidimensional integration을 찾아야 하기 때문에 복잡하다. MLE는 최대값을 찾기 위한 미분을 하게 되므로 비교적 간단하다.
2) Interpretability
해석하는 데에 있어서도 ML solution이 더 간단하다.
3) Confidence in the prior information
문제에 대해 더 많은 정보를 사용해서 구하는 것이 Bayes 방법이다.
최종 시스템에는 세가지 classification 에러 원인이 있다.
1) Bayes or Indistinguishability(판별불가) error
density가 겹쳐진 부분 근처에서는 어떤 것을 선택해야 하는지에 대한 어려움이 존재한다. 어떤 model을 잡더라도 제거될 수 없는 본질적인 특성이다.
2) Model error
우리가 정한 모델이 데이터의 실제 모델이 아니라면, 위에서는 가우시안이라 가정했는데, 그 분포가 가우시안이 아니라면 생길 수 있는 에러가 존재한다.
3) Estimation error
유한한 샘플에 대해 추정한 결과이다보니, Model이 맞더라도 생길 수 있는 오류가 존재한다.
[PRML 2.3.9 Mixture of Gaussians]



위에서 Model error를 줄이기 위한 그림이다. 위에서 가정했던 하나의 가우시안으로 나타낸다면 일어날 수 있는 에러가 위 그림으로 표현되어 있다. 서로 다른 분포로 이루어져 있다고 생각한다면 model을 더욱 좋은 model로 이끌 수 있을 것이다. k개의 가우시안을 linear combination하고, 그 계수가 합쳐서 1이 됨을 가정하고 풀게될 것이다.
3.7 Problems of Dimensionality
실제 상황에서는 features의 개수가 100개 이상을 가질 수 있다. 차원이 커질수록 좋은 classfier가 되겠지만, 그에 따른 문제도 분명히 존재한다. 크게 두 가지 이슈가 존재하는데, 1) 분류의 정확도가 차원에 어떻게 연관되는가와, 2) 계산이 복잡한 점이다.
1) 차원이 커지면 분류의 정확도가 커지는가.

$p(x|\omega_j) ~ N(\mu_j, \sum)$ ($j = 1, 2$)일 때, 즉 $\sum$이 같은 두 클래스에 대해 사전 확률이 같다면 구할 수 있는 Bayes error이다. 여기서, r은 mahalanobis distance이고, conditionally independent case이므로 아래와 같이 쓸 수 있다.

따라서, 에러의 확률은 r이 증가함에 따라 감소하고, 이는 dimension이 커지면 오류가 감소함을 뜻한다. seabass와 salmon을 구분하는데 있어서 만약 길이만으로 고려를 하고 있었다면, 밝기나 무게라는 조건이 추가된다면 이 둘을 구분하는데 있어서 정확도가 올라간다는 것은 당연하다.
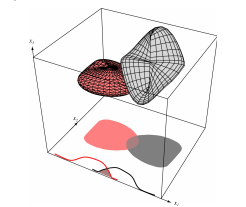
1차원에서는 겹치는 부분이 많고, 2차원으로 가면 그 부분이 줄어들고, 3차원에서는 겹치는 부분이 존재하지 않는다. 차원이 커질수록 좋은 classfier가 된다는 것, error가 줄어든다는 점을 표현한 것이다. 하지만 차원이 커질때 마냥 좋은 것은 아니다. 연산이 복잡해져 시간, 비용이 늘어난다는 점도 있지만, 조금 더 근본적인 문제들이 존재한다.
1)처음 가정했던 모델이 틀렸거나, 2) 차원이 커지면서 많은 샘플의 수를 필요로 하게 되는데 샘플의 수가 유한하기 때문에 분포들이 정확하게 추정이 되지 않거나, 3)추정하는 과정에서 오류가 발생할 수 있다. 따라서 어떤 선을 넘기면 새로운 feature를 추가하더라도 그때부터는 성능이 좋아지지 않는다. 오히려 실제 많은 사례에서 오히려 안좋은 classfier가 된다는 점이 자주 관찰되어왔다고 한다.
2)계산 복잡성

computer science에서 자주 쓰는 big oh를 써서 표현한 것이다. 모든 $x>x_0$에 대해 $|f(x)|\leq c|h(x)|$를 만족시키는 상수 c와 $x_0$가 존재한다면, 이 f(x)는 h(x)의 big oh이다. 이 값이 exponential하게 설정되어 있다면 연산량이 디멘젼이 커짐에 따라 급속하게 늘게 될 것이다. 위 식에서는 연산량이 O($\d^2n$)이라 할 수 있는데, d가 늘어남에 따라 많은 비용을 지불하게 된다.
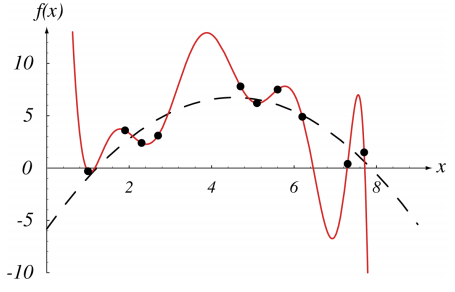
위의 그림에서 빨간선은 10차 curve이고, 점선은 2차 curve이다. 데이터들을 보면 2차 함수가 전체적인 데이터의 양상을, 실제 true데이터에 가까울 수 있다는 점이 눈에 보인다. 하지만, 위의 10개의 데이터에 정확하게 맞춘 것은 10차식으로 나타낸 함수이다.
결국 위 그림에서 말하고 싶은 점은 샘플들에 대한 정확한 fitting이, 전체 분포에 대한 정확한 fitting이 아닐 수 있다는 점이다. 오히려 샘플에 대해 덜 정확하게 하는 점이 전체적인 데이터를 더 정확하게 나타내는 점일 수도 있다. 이를 overfitting이라 한다.
3.8 Component analysis and discriminants
위에서 언급한 차원의 문제, 차원이 증가함에 따라 생기는 문제는 간단하게 차원을 줄임으로써 해결될 수 있다. 이 장에서 그 부분을 다뤄본다.
[Principal Component Analysis(PCA)]
우선, 하나의 벡터로 n개의 d-demension의 샘플 $x_1,\cdots , x_n$의 모든 벡터들을 나타내보자. 하나의 벡터로 표현하기 위해, 다른 벡터들간의 사이 거리가 최소가 되도록 하는 것을 목표로 다음 식을 세운다.

내가 표현하고자 하는 벡터는 $x_0$이고, 다른 벡터들간의 사이 거리가 최소가 되도록 하는 벡터를 구하면되는데, 이는 $\partial J_0 / \partial x_0 $의 값이 0이 되는 점을 찾으면 될 것이다. 그 결과는 $x_0$값이 샘플의 산술 평균 값이 되는, $x_0=m$에서 $J_0$가 최소가 된다.
이제, 샘플들을 어떠한 단일 벡터로 나타내는 것이 아닌, 선으로 나타내보자. 이 역시 마찬가지로 선에서 떨어진 거리가 최소가 되도록 하는 선을 구하면 된다고 생각하면 된다. 그를 위한 작업으로, 나타내고자 하는 선을 e로 정해져 있다고 하고, 그 거리를 최소로 하는 값이 무엇인지 부터 알아볼 것이다. 즉, 고등수학에서 배우는 점과 직선사이의 거리를 어떻게 벡터로 표현해낼 수 있는지를 보는 것과 같다고 보면 된다.

샘플의 각각의 $x_k$벡터들을 위와 같이 표현할 수 있다. m은 위에서 구한 샘플들의 평균, e는 나타내고자 하는 선이다.
m과 e는 모두 같은 방향의 벡터가 될 것이라는 것을 알 수 있고, (m은 e선위를 지날 것이다.) 위에서 표현한 x는 $x_k$벡터들을 e벡터에 projection한 식이다.

결국 점과 직선사이의 거리를 구하기 위한 성분은 projection한 성분에 대해 구해줄 수 있음을 보여준다. 위에서 구한 $a_k$는 각각의 벡터들이 어떻게 e위에 projection될 수 있는지에 대한 식이다.

위 그림과 같이 빨간점에서 초록색 점으로 projection하여 결국 우리가 최소로 만들어야할 것은 빨간색과 초록색 점 사이 거리의 합을 최소로 만들어야 한다.

Scatter(산포) matrix를 사용하게 되는데, 사실 분포에 대한 식이 평균에서 얼마나 떨어져 있느냐에 대해 궁금해서 얻은 값이기 때문에, 위 식에서 scatter matrix를 사용하는 것은 언급한 목적과 같다. 위에서 구한 $J_1$에서 $\sum_{k=1}^n$의 항은 e에 따라 변하지 않는 값이다. 지금은 어떤 선으로 샘플들 $x_1,\cdots,x_n$을 잘 나타낼 수 있는지, e를 구하는 것이기 떄문에 제거 한다면 $e^tSe$가 최대가 되도록 해야 한다.

이는 Lagrange optimization을 사용하여 풀었다. 결국에 얻을 수 있는 식은, 우리가 처음 목적했던 데이터들을 가장 잘 나타내는 선을 나타내보자 하는 선을 e라 했을 때, 그 선 e는 scatter 벡터의 eigenvector가 된다는 것이다. 이 값이 최대가 되려면 eigenvalue값이 최대가 되야 하고, eigenvalue값이 높은 순서대로 정렬했을때 가장 높은 eigenvalue와 연결되는 eigenvector가 결국 e가 된다는 것이다. 높은 순서대로 정렬했으므로, 만약 n차원의 데이터를 2차원으로 낮춘다면, eigenvalue값이 높은 2개의 값에 대응되는 eigenvector값으로 나타낼 수 있을 것이다.
[참고] Lagrange optimization


위는 참고가될 수 있는 라그랑지식이다. 왼쪽 식에서 스칼라 값 함수 f(x)의 극 값의 위치 $x_0$를 찾는다고 하는 것이 목적이다. g(x)=0의 형태로 표현될 수 있다고 한다면, f(x)는 왼쪽 식을 통해 얻어낼 수 있다. 여기서 $\lambda$는 Lagrange undetermined multiplier이고, 이를 위해 미분하여 오른쪽과 같은 식으로 만들어준다. 이를 위해 취한 작업이 $e^te-1$을 추가해준 것이다.

위에서 설명한 것과 같이, scatter의 eigenvalue가 높은 순서대로 정렬하여 높은 순서대로 벡터를 정하여 차원을 낮출 수 있다. 위 그림에서는 3차원이므로 3개의 eigenvalue가 나오게 되고, 그 값이 작아보이는 pc3(이 방향으로 분산이 작다)에 대해 소거를 하고, PC1과 PC2만 가지고 샘플들을 표현해준 것이다. (=projection 해준 것이다.)
[Fisher linear discriminant]
하지만, 우리가 이렇게 하는 목적은 classfication에 있는데, 좋은 classfier가 되지 못한다면 소용이 없을 것이다. 이를 위해 Fisher linear disciminant 방법이 있다.

위 그림에서 분산이 큰 부분은 보라색 선에 해당하는 벡터이다. 하지만 여기에 벡터들을 projection시키면 점들이 겹치게 될 것이다. 하지만, 초록색 선에 데이터들을 projection시킨다면 데이터들이 위쪽엔 파랑색으로, 아래쪽엔 빨강색으로 뭉치게 될 것이다. 위에서 목적했던 eigenvalue가 높은, 즉 분산이 높은 벡터를 선정했을 때의 단점이 존재하는 것이다.
따라서, 위에서 보았던 데이터를 단순히 잘 표현해내는 벡터만으로는 한계가 있는 것이다. 이에 우리는 어떤 수치를 갖고 판단할 수 있는지에 대해 고민해보아야 한다.

이 그림도 역시 왼쪽 것보단 오른쪽의 벡터를 선택했을 때 조금더 분류가 쉽게 될 것이다.
Fisher linear discrimination은 클래스에 속하는 샘플의 평균간의 거리가 멀어야 한다고 생각하고, 각각의 클래스에 속하는 샘플안의 편차는 작아야 한다고 생각한다. 즉, 다른 클래스끼리는 멀었으면 좋겠고, 같은 클래스끼리는 뭉쳐있으면 좋겠다라는 생각인 것이다. 이에 따라 아래와 같은 정의를 거친다.

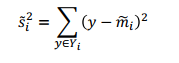
위에서 적은 다른 클래스간의 거리(클래스간의 평균 차)는 커야하고, 같은 클래스간의 분산은 작아야 하므로,

이 값이 최대가 되도록 만들어야 할 것이다.
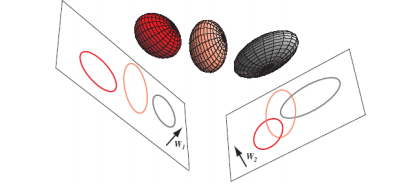
이 예시에서도 3차원의 공간을 2차원에 projection을 시키는데, 어떤 평면에 사영시키는지에 따라 classfier의 성능이 달라질 것이다. 또, 3차원에서 구별할 수 있는 것을 2차원에서도 완벽하게 구현해낼 수 있다면, projection시키는 것이 좋다고 판단할 수 있을 것이다.(위에서 언급했던 계산상의 문제 등)
[Expectation-Maximization(EM)]

샘플들을 두 개의 class로 나누고자 한다. 이 때 클래스를 파란색 원과 빨간색 원으로 나타낼 것이다.
a) 우리는 샘플에 대한 정보가 없으므로, 임의로 두개의 원을 그려 class를 나눠 보았다.
b) 나눈 영역과 가까운 영역을 본인의 클래스라고 주장하며 파란색 원과 가까운 점들은 파란색,
빨간색 원과 가까운 점들은 빨간색 영역이 되어 샘플들을 두 개의 클래스로 나눈다. (데이터가 집합에 속해진다.)
c) 이렇게 구별된 파란색과 빨간색 점에 대해 MLE와 같이 데이터를 잘 표현할 수 있는 평균과 분산을 구한다. 이에 scatter는 그려질 것이다.
d) b에서 했던 것과 같이, c에서 그린 평균과 분산에 의해 그려진 타원으로 파란색 타원과 가까이 있는 점들은 파란색,
빨간색 타원과 가까이 있는 점들은 빨간색으로 다시 칠한다.
e) c에서 했던 것과 같이, 파란색과 빨간색 점에 대해 MLE와 같이 데이터를 잘 표현할 수 있는 평균과 분산을 구해 scatter을 그린다.
f) 위 과정을 반복하면 f를 얻는다.
우리가 (a)만 보고, 두 클래스로 나눈다고 하면, 위의 영역과 아래의 영역으로 나누는 것이 당연해보인다. 이를 프로그래밍으로 어떻게 구현할지에 대한 방법론을 제시한 것이다. 결과 역시 우리가 눈으로 보고 클래스를 나눈 것과 비슷해 보이는 것을 알 수 있다. 잘 분류가 되었다고 볼 수 있을 것이다.
Reference
- pattern classification by richard o. duda
'Review > Pattern Classification' 카테고리의 다른 글
| [패턴인식]Chapter 4.5~6 The Nearest-Neighbor Rule (0) | 2022.10.18 |
|---|---|
| [패턴인식]Chapter 4.4 k_n-Nearest-Neighbor Estimation (0) | 2022.10.18 |
| [패턴인식]Chapter 4.3 Parzen Windows (0) | 2022.10.13 |
| [패턴인식]Chapter 4.1~2 Nonparametric techniques (0) | 2022.10.13 |
| [패턴인식]Chapter 2. Bayesian decision theory (0) | 2022.09.27 |



