(김경환 교수님의 자료와 수업을 통해 제작되었습니다.)
4.5 The Nearest-Neighbor Rule
4.4절에서 언급한 posteriori를 직접 구할 수 있는 방법에 대해 알아보고자 한다.
The Nearest-Neighbor rule은 $D^n={x_1,\cdots,c_n}$으로 n개의 샘플들을 어떠한 공간에 흩뿌린다고 하자. 그 다음, 테스트 점 x를 공간에 나타냈을 때, 그 x에 대해 가장 가까운 점을 고르고, 그 점에 해당하는 클래스를 선택하자는 것이 기본 생각이다. 즉, 각각의 점들이 영역을 나타내게 되어 그 점이 갖는 영역 안에 들어가면 그 점에 해당하는 클래스로 고르자는 것이다. 이 때 주변의 점을 볼 때 k개를 본다고 한다면, 홀수개의 샘플을 비교하여 $\omega_i$를 결정한다고 한다.

x'이 x에 충분히 가깝다면 나타낼 수 있는 식이고,

와 같이 공간을 분해하는 것을 Voronoi 분할이라고 하는데, 각 점에 대해 본인의 공간을 가지도록 분할하는 것이다.

$P(\omega_m|x)$가 1에 가까울 때 Nearest-neighbor 추정은 거의 항상 Bayes 선택과 같아진다. 또한, $P(\omega_m|x)$가 1/c에 가깝다면, 모든 클래스가 동등한 확률을 가지면 Neareat-neighbor방법과 Bayes 선택은 거의 같지 않지만, 에러 확률은 둘다 1-1/c이다. 이에 생각보다 에러 확률이 높지 않음을 알 수 있고 다음과 같은 부분도 볼 수 있다.

The Nearest-Neighbor Rule은 bayes error의 두배는 되지 않는다는 결론을 얻은 그래프이다. $P^*$은 Bayes error이고, P는 이번 장에서 다루는 Nearest-Neighbor error이다. 즉, bayes error의 1~2배 사이에 있다는 것을 보여준다. 앞장에서 했던 추정들보다 간단한 추정임에도 높은 정확성을 보이는 것은 놀라운 결과라 할 수 있다.
[The k-Nearest-Neighbor Rule]

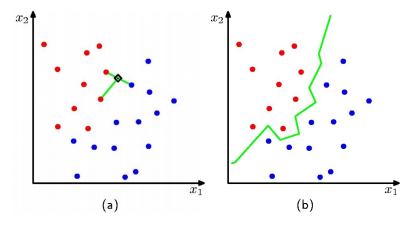
알고자 하는 x에 대해 그 주변 샘플을 조사한 뒤, 가장 가까운 샘플 k개를 선택하여 가장 많이 속한 클래스를 결정하게 된다. 주변 샘플을 보는 개수 k개는 홀수개를 선정하고, 이 기준에 따라 boundary를 오른쪽 초록샌 선과 같이 지정할 수 있다. 초록색 선 기준으로 왼쪽은 빨강색의 클래스, 오른쪽은 파랑색의 클래스로 분류될 것임을 알 수 있다.
당연한 얘기이겠지만, 주변 샘플을 많이 볼수록 error rate가 줄어들 것이다.


왼쪽 그림은 빨간색 선으로 갈수록 error rate가 줄어드는 것을 볼 수 있는데, 이는 분류할 때 주변 샘플을 1,3,9,$\cdots$으로 더 많은 주변 샘플을 보고 판단하기 때문이다.
오른쪽 그림은 k=1부터 31까지 보이는 샘플에 따른 bounday이다. k=1일 때에는 가장 가까운 샘플의 클래스를 선정하는 것이기 때문에 주어진 샘플에 대해서는 완벽하게 fitting이 되어 있지만, 새로운 샘플이 주어졌을 때에는 적용이 되지 않을 것이라는, overfitting을 예상할 수 있을 것이다. k=31로 갈수록 generallization이 되어 초록색 점이 있는 주변에도 파랑색의 클래스로 판단하는 것을 볼 수 있고, 전체적인 그림을 볼 수 있다는 점에서 error rate가 줄어들 것이다.
하지만, x를 기준으로 가장 가까운 샘플을 보게 되면, 거리의 계산에 부담이 생기기 마련이다. 주변의 샘플과 비교하는 개수가 많아질수록, k가 커질수록 부담은 더 커질 것이다. 우선, 거리에 대해 정의해보자.
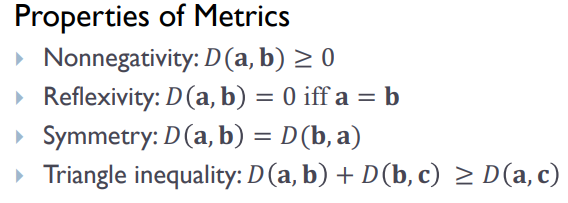
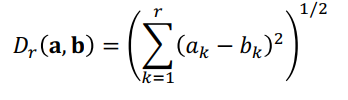
properties of metrics에 언급된 부분은 norm공간에 대한 설명이라고 할 수 있다. 이는 거리개념을 내포하고 있고, 두 벡터 사이의 차이에 대해서도 조사할 수 있다. 많은 샘플 수에 대해 모든 거리를 계산하는 것은 어려울 수 있으므로, 아래의 방법들로 계산상의 부담을 줄여주고자 한다.
(1) computing partial distance
x를 기준으로 가장 가까운 샘플에 대해 보고자 하는 것이므로, 계산했던 값 중에서 min값을 고려하여, 그 값보다 큰 샘플과의 거리는 계산하지 않는 것이다. 계산하는 과정에서 값이 너무 커지면 계산을 중단하는 것이다.
(2) Prestructuring
샘플끼리도 각각 영역을 정하여 그 영역을 대표하는 샘플 하나만을 가지고 x와 거리계산을 한다. 거리가 가까운 것으로 판단되는 몇개의 영역에 대해서만 영역안의 모든 샘플과의 거리 계산을 진행한다. 이 경우 영역과의 경계에 있는 샘플이 선택 된다면 가장 가까이 있는 점에 대해서 조사하지 못하는 경우가 생길 수 있지만, 이는 계산 복잡도와 어느정도의 trade-off가 될 것이다.
(3) Editing the stored prototypes
샘플들이 x에 대해 굉장히 많이 겹쳐있고, 같은 레이블을 갖는 샘플들의 거리가 모두 비슷한 값을 갖는다면, 그 값들 중에도 대표로 하여 계산하는 것이다. 알고리즘은 다음과 같다.

4.6 Metrics and Nearest-Neighbor Classification
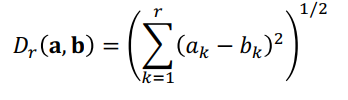
위 4.5장에서 거리에 대해 정의하고, norm공간에 대해서 언급하였다. 언급한 Euclidean distance는 특정 곤간의 좌표들을 스케일링하는 경우에 취약하다.

위와 같은 경우는 $x_1$축으로 $\alpha$배 만큼 수축한 것이다. 위 그림은 $\alpha=1/3$이다. 왼쪽의 그래프에서 x에 대해 가장 가까운 샘플은 검정색이었지만, 오른쪽 그래프에서는 가장 가까운 점이 빨강색이다. 스케일링에 따라 달라질 수 있는 것을 보여주는 것이다. 만일 각 차원에서 데이터 범위에 큰 불균형이 있다면, 같은 범위 내에 있도록 rescale해주는 것이 일반적일 것이다.
[Minkowski metric]
d-dimensional pattern에 대한 거리 Minkowski metric은 다음과 같이 나타낼 수 있다.


이는 $L_k$ norm이라고 불리기도 한다. L2 norm은 유클리드 거리이고, L1 norm은 Manhattan or city block 거리라고 부르기도 한다. 위 그림 중 아래에서는 k가 커짐에 따라 원점으로부터 거리가 1.0으로 같은 점들을 모아놓은 것이다.
[Tanimoto Metric]

Tanimoto Metric은 분류학에서 주로 사용되며, 두 집합 간의 거리가 위와 같이 정의된다. n1과 n2는 각각 S1과 S2의 원소의 개수이며, n12는 S1과 S2의 교집합에 대한 원소의 개수이다. 이 metric은 두 개의 패턴 혹은 feature가 같은 문제들에 대해 유용하게 쓰인다.
4.5장에서는 posteriori를 직접 구할 수 있는 방법에 대해서 알아보았다. 앞에서는 간접적으로 prior와 likelihood를 계산하여 구하는 방법을 사용하였지만, 이번 장에서는 그러지 않았다. 주어진 x에 대해서 그 값의 주변 샘플들을 보고, 가장 많이 속하는 레이블을 선택하는 것이 원리였다. 간단한 원리임에도, error rate가 높지 않은 것은 놀라운 결과라고 생각할 수 있고, 주변의 샘플을 많이 보는 것은 error rate가 줄어들게 하였다. 하지만, 계산상의 부담은 커지게 되는데, 이 부담을 줄여줄 수 있는 방법 3가지를 이번 장에서 언급해 주었다.
4.6장에서는 거리에 대한 정의를 어떻게 하는지에 대해 알아보았고, 다양한 정의가 존재하는 것을 볼 수 있었다. 상황에 따라 맞는 거리의 정의를 사용하면 될 것이고, 이들은 norm공간의 정의를 만족하는 metric이 될 것이다.
Reference
- pattern classification by richard o. duda
'Review > Pattern Classification' 카테고리의 다른 글
| [패턴인식]Chapter 5.3 Generalized Linear Disciminant Functions (0) | 2022.11.02 |
|---|---|
| [패턴인식]Chapter 5.1~2 Linear Discriminant Functions (0) | 2022.11.02 |
| [패턴인식]Chapter 4.4 k_n-Nearest-Neighbor Estimation (0) | 2022.10.18 |
| [패턴인식]Chapter 4.3 Parzen Windows (0) | 2022.10.13 |
| [패턴인식]Chapter 4.1~2 Nonparametric techniques (0) | 2022.10.13 |



