[패턴인식]Chapter 4.1~2 Nonparametric techniques

Quietly_ 2022. 10. 13. 00:09

(김경환 교수님의 자료와 수업을 통해 제작되었습니다.)

4.1 Introduction

3장까지 살펴보았던 MLE, bayes estimation은 분포의 형태는 알고 있다고 가정하고 문제를 접근하였다. 이번 4장에서는 분포가 arbitrary하더라도 posterior density function을 구해보고자 하는 것이 4장의 목적이 된다.

1) likelihood를 non-parametric form으로 구해보자.

2) $p(\omega_j|x)$를 직접 구해보자

위 두 가지 접근 방법을 갖고 4장을 접근해보는 것이다.

4장에 들어가기 전, 깡통에 fish를 넣는 예시를 들어보도록 하겠다. 생선들을 분류하기 위해 깡통을 준비하고, 분류 기준에 맞게 x축 위에 깡통을 여러개 세워두고, 각각의 깡통에 넣는 것이다. 우리는 통안에 있는 생선들의 수를 세어 smooth한 곡선으로 생선에 대한 분포를 추정하게 될 것이다. 그렇다면, 이 조건에서 깡통의 크기를 작게 할수록 우리가 선택한 조건 x와 딱 맞는 density를 알 수 있게 된다. 만약 feature가 13.5~14.5면 들어가는 깡통이 있고, 내가 14.33인 feature를 얻었다면, 13.5~14.5의 분포를 보고 알아낼 수 있는 것이므로 신뢰성이 떨어지게 되는 것이다. 즉, 14.33일 때에만 들어가는 깡통을 따로 만들 때 가장 높은 정확성을 띄게 되는 것이다. 하지만 이는 굉장히 많은 샘플을 요구하므로, 어느정도 부피를 갖고 깡통을 만들게 된다. 깡통이 일정하더라도, 각 깡통안에 있는 생선의 수가 많을수록 신뢰성은 높아진다. 깡통이 5개인 상황에서 10마리정도만 들어가 있다면, 남은 생선에 대해서 고려하지 못한 부분이 많으므로 신뢰성이 떨어진다.

위에서 설명한 부분에서 생선의 전체 마리수를 n, 깡통의 부피를 $V_n$으로 정의하고, 깡통을 $R_n$이라고 할 수 있고, $R_n$에 속한 생선의 수를 $k_n$이라 할 수 있다.

4.2 Density estimations

P는 벡터 x가 영역 R에 들 확률을 말한다. P는 p(x)의 averaged version of density function이라고 할 수 있다. 우리는 P를 추정하여 smooth한 p의 값을 추정할 수 있다. n개의 샘플 $x_1,\cdots, x_n$은 p(x)에 따라 independent하고, identically distributed되도록 뽑는다고 하자. 이 n개의 데이터 중에 k개가 R에 포함될 확률은 binomial law에 의해 주어진다.

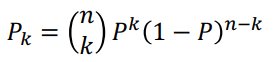
E[k]는 k에 대한 기대값이다. 이 추정은 n이 클수록 날카로운 피크값을 가지며, 더욱 정확한 값을 갖게 된다.

위 그림에서 n이 커질수록 피크값이 날카로워지는 것을 확인할 수 있다. V는 결정하고자 하는 영역 R의 부피를 뜻한다.

우리는 R영역 내로 샘플들을 조건에 맞게 집어 넣게 될 것이다. 하지만, R의 영역의 부피가 0이 아닌 이상, 우리는 space-averaged 값만을 얻을 수 있을 것이다. 샘플의 개수가 무한대일 수는 없지만, 우리가 원하는 지향성 내에서 n이 무한대로 접근할 때 값이 어떻게 수렴하기를 원하는지에 대한 조건을 알아보자.

왼쪽부터 하나씩 살펴보면, 첫번째 조건은 앞에서 언급했던 R의 영역이 0으로 수렴하는 것이다. 공간에 대한 확률이 아닌, 그 점에서의 확률을 얻고자 하므로 R의 부피는 0으로 접근하고 싶어할 것이다.

두 번째 조건은 그 R에 속한 샘플의 개수가 무한히 많아질 때 100%의 신뢰성을 갖게 되므로, 두번째 조건이 추가된다.

세 번째 조건은 전체 샘플 수 n이 커지는 증가율이 각 R에 속하는 샘플들의 증가율보다 높아야 한다는 조건이고, 전체 샘플 수가 월등히 더 많아야 한다는 점을 내포한다.

이러한 조건들을 만족시키기 위해 이번 장에서는 크게 두가지 조건을 제시한다.

1) 부피를 $V=1/\sqrt{n}$으로 R의 영역을 줄이는 방법 (Parzen Windows)

2) $k_n=\sqrt{n}$으로 영역 안에 존재하는 샘플 수를 늘리는 방법($k_n$-nearest-neighbor)

위 두가지 방법으로 다음 장들을 전개해 나간다.

우리는 결국 샘플의 수가 유한으로 정해진 상황에서, 높은 신뢰값을 갖는 확률을 얻기 위해 어떠한 방향성을 갖고 데이터를 분류해나가야 하는지에 대한 부분을 알아보고 싶은 것이다.

Reference

pattern classification by richard o. duda