[패턴인식]Chapter 2. Bayesian decision theory

(김경환 교수님의 자료와 수업을 통해 제작되었습니다.)

2.1 Introduction

  Bayesian decision theory는 패턴인식을 하기 위한 통계적인 접근이다.

이 접근은 확률에 의한 결정으로 분류를 하게 되고, 이에 수반되는 비용이 고려되야 한다.

또, 이는 모든 값들이 확률에 대한 term으로 나타낼 수 있어야 하고, 모든 값들을 알고 있다고 가정한다.

따라서 이번 장에서는 확률값을 갖고 어떤 관점으로 해석할 수 있는지를 배울 것이다.

서브챕터에서는 확률 값들을 모르는 상황에서는 어떻게 다뤄져야 하는지에 대해 배운다.

 

 

  1장에서 사용했던 sea bass와 salmon이 등장하게 된다. $\omega$를 State of nature라고 부르며,

$\omega = \omega_1$를 sea bass, $\omega_2=\omega_2$를 salmon이라고 하자.

 

[Priori probability]

  우리가 sea bass와 salmon를 7:3으로 계속 잡아왔다고 한다면, 다음에 올 생선에 sea bass가 나올 확률은 70%라고 볼 수 있고, salmon이 잡힐 확률은 30%라고 봐도 될 것이다. 이러한 확률을 Priori Probability(간단하게 prior)라고 한다. 

예시와 용어로 알 수 있듯이, 우리가 계산을 하여 구하지 않더라도 사전에 이미 알고 있는 정보를 포함하는 확률이다.

만약 현재 seabass가 바다에 굉장히 많아 95:5로 seabass와 salmon이 존재한다라는 정보가 있다면,아무런 계산을 거치지 않고, 어떤 생선을 seabass라고 분류 했을 때의 정확도가 95%가 될 것이다. 따라서 Priori probability는 중요한 정보가 될 것이다.

 

[Decision Rule]

  Priori probability는 sea bass가 잡힐 확률 $P(\omega_1)$와$ P(\omega_2)$로 나타낼 수 있다. 이 값들의 합은 1이 된다.생선이 왔을 때 sea bass와 salmon을 구분해야하는 상황이 오게 된다면, 잘못 선택했을 때의 비용, 상황들이 존재를 할 것이다.  또, salmon을 seabass로 판단했을 때, seabass를 salmon으로 판단했을 때의 지불비용은 실제로는 다를 것이다. 이를 제외하기 위해 지불 비용이 모두 같다고 가정하면, $P(\omega_i)$가 가장 큰 i번째의 state of nature라고 결정해야 한다.

 

[Class-conditional probability density function]

  이제 생선을 잡아서 특징을 잡아 seabass와 salmon으로 분류해보고자 한다. 밝기를 기준으로 둘을 구분하고자 했을 때, salmon은 밝은 색들의 분포가 많았고, seabass는 어두운 색들의 분포가 많았다고 한다면, 우리는 밝은 색의 생선을 보고 salmon일 것이다 라고 어느정도 유추할 수 있을 것이다. 여기서, 우리가 알아낼 수 있는 정보는 salmon중에 밝은게 몇마리인지, 어두운게 몇마리인지를 알 수 있고, seabass도 같은 정보를 알아낼 수 있을 것이다. 이를 Class-conditional probability density function으로 나타낼 수 있고, $p(x|\omega_i)$으로 나타낸다. $p(x|\omega_1)$은 선택된 $\omega_1$, seabass 중에서 x, 밝기 성분(밝거나 어둡거나, 혹은 0~255의 밝기값)을 가질 수 있는 확률에 대한 값이다.

 

[Bayes formula]

  하지만, 우리가 알고자 하는 부분은 생선을 분류하는 것이고, 밝기 값으로 분류를 한다면 밝은 생선 혹은 어두운 생선이 주어졌을 때, 이를 salmon 혹은 seabass라고 구별할 수 있어야 한다. 이 확률은 $P(\omega_j|x)$이고, 앞에서 구할 수 있었던 $p(x|\omega_1)$ 값을 이용하여 구해낼 수 있어야 한다. 또한, 앞에서 언급했던 prior과 같이 구할 수 있을 것이라는 건 앞의 내용을 본다면 자연스럽게 도출될 수 있을 것이다.

  따라서, 우리는 Bayes formula를 이용할 것이고, 수학적으로는 쉽게 나타낼 수 있는 식일 수 있지만, 의미적으로는 패턴인식의 본질적인 의미를 내포하고 있다고 해도 과언이 아닐 것이다. 우리는 패턴인식에서 $P(\omega_j|x)$, 값이 주어졌을 대 분류를 하는 것이 궁극적인 목표이고, 이를 위해 $p(x|\omega_1)$와,$P(\omega_j)$를 구하는 과정을 배울 것이다. 이에 대한 식은 다음과 같다.

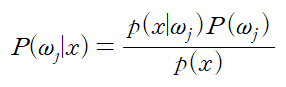
  이 식은 다음과 같이 나타낼 수 있다.

posterior= $\frac{likelyhood \times prior}{evidence}$

  결과적으로 우리는 prior probability, likelihood를 통해 우리가 구하고자 하는 posteriori probability를 구할 수 있었다.

 

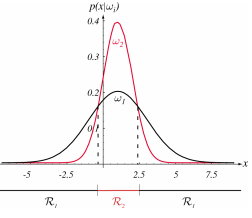
  위 사진에서 왼쪽은 우리가 구할 수 있는 그래프이고, 오른쪽은 우리가 알고자 하는 그래프이다. 오른쪽 그래프에서 x가 정해지면 $\omega$를 정할 수 있게 된다. 위 그래프에서 x가 14라면 $P(\omega_1)>P(\omega_2)$이므로, $\omega_1$을 택하게 될 것이다. 이는 Decision Rule을 사용하게 될 것이다.

 

[Bayes Decision Rule]

  위에서 우리는 $\omega_1 or \omega_2 $를 결정할 수 있었다. 이에 따른 error에 대한 확률을 구할 수 있게 되고, 위와 같은 에러를 갖게 된다.

  우리는 $P(error|x)$을 최소로 하는 결정을 내릴 수 있을 것이고, 전체 에러의 합을 다음과 같이 나타낼 수 있다.

  $P(\omega_1|x) > P(\omega_2 |x)$인 경우 $\omega_1$을 선택할 수 있고, 반대의 경우 $\omega_2$로 결정할 수 있게 된다. 이에 따라 $P(error|x)=min[P(\omega_1 |x), P(\omega_2 |x)]$로 에러가 정해진다. 

  Decision Rule에서 알 수 있듯이, posterior probabilites는 중요한 역할을 하게 된다. 여기서, Bayes formula를 사용하면 우리가 구할 수 있는 term들로 나타나게 된다. 여기서 evidence, $p(x)$에 관한 항은 결정하는데 있어서 중요하지 않은 term이기 때문에 $p(x)$를 제외하고 고려하면 다음과 같이 정할 수 있다.

2.2 Bayesian Decision Theory - Continuous Features

[Generaliztion of the Bayesian Theory]

  Baysian Theory를 일반화 하기 위한 방법으로 크게 4가지의 방법이 있다.

  1) 둘 이상의 feature를 이용한다. 

  위에서는 fecture를 하나만 이용해서 Bayes theory를 적용해 주었다. 따라서, scalar x를 feature vector $x$로 변경한다.

  $x$는 $R^d $ 공간에 존재한다.

 

  2) 셋 이상의 states of nature를 사용한다.

  이 역시 $\omega_1$ $omega_2$를 제외한 다른 state of nature를 포함할 수 있다.

  ${\omega_1 , \cdots , \omega_c }$ 를 정의할 수 있다.

 

  3) $\omega$를 결정하는 것 이외의 상태를 고려하는 것.

  선택이 애매한 경우에는 선택을 포기하는 경우의 수도 고려할 수 있을 것이다. 다음과 같이 $\theta$를 정해두고, 그 값보다 작은 경우 reject region으로 정하여 decide하는 경우의 확률을 높일 수 있을 것이다.

  4) 선택 후 액션을 취했을 때 생길 수 있는 손실을 고려.

  seabass를 salmon으로 판단했을 때, salmon을 seabass로 판단했을 때 생기는 손실은 다를 것이다. 이를 고려하여 분류한다. $\lambda(\alpha_i |\omega_j )$ : $\omega_j$를 $\omega_i$로 판단하여 행동을 취했을 때 생기는 손실. 이 람다를 선택하는데 고려해주어야 한다. 

 

[Conditional risk] 

[Overall risk, Bayes risk]

  Overall risk를 최소화 하기 위해 conditional risk를 최소화 시켜야 하고, 그렇게 구한 minimum overall risk를 Bayes risk라 한다.

[Two-category Classification]

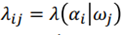
  이를 결정하기 위해 다음과 같이 결정한다.

 

  모두 $\omega_1$을 택할 수 있는 조건이 될 것이다. 마지막 식을 얻기 위해 위와 같은 과정을 거쳤다. 

  마지막 부등식에서 우항은 x에 관계없는 일정 thresh hold값이라고 할 수 있고, 이 임계값을 $\theta$라 하면, 이 값보다 더 큰 경우에 $\omega_1$을 선택하면 된다. 좌항은 likelihood ratio라 한다.

 

2.3 Minimum-Error-Rate Classification

[Zero-one loss function]

  위와 같이 판단에 대한 손실, 비용이 1이라고 해보자. (판단이 맞을 땐 손실이 0) 이를 zero-one loss function으로 설정하는 것이다. 

  $R(\alpha_i |x)$, conditional risk가 최소가 되기 위해 posterior probability를 최대로 만드는 결정을 해야한다. 

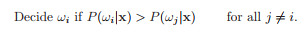
2.4 Classifiers, Discriminant Functions and Decision Surfaces

[Multi-Category Case]

  pattern classfier를 표현하는 데에는 많은 방법들이 있다. 가장 유용한 방법 중 하나는 discriminant functions $g_i (x)$로 표현하는 것이다. 

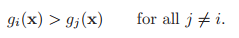
  여러 클래스 중 하나의 클래스를 선택하기 위해 discriminant function을 사용하게 된다. disriminant function 값을 최대로 하는 i번째의 클래스가 선택이 된다.

  Classfier에 사용하는 discriminant function은 여러가지 형태로 나타낼 수 있다.

  이는 딥러닝에서 activation 함수를 Relu, sigmoid등을 사용할 수 있는 것과 비슷하다고 생각한다. 용도에 따라 다르게 사용될 수 있다.

 

  이 식에서는 posterior probability를 discriminant function으로 사용하였다. 위 두번째식에서 3번째 식으로 넘어올 수 있는 것은 ln은 monotonically increasing function이기 때문이고, ln을 취하면 곱을 합으로 이끌어낼 수 있는 장점이 존재한다.

[The Two-Category case]

  두 개의 카테고리로 분류하는 경우이다. 이는 Dichotomizer라고도 한다.

 

  두 개의 클래스 밖에 없으므로, g(x)의 부호로 결정할 수 있다. g(x)>0이면 $\omega_1$을 선택한다. 

2.5 The Normal Density

  분석적으로 다루기 쉽게 하기 위해, normal 혹은 gausian density가 많이 사용된다.

[Expection]

  아래는 discrete set D에 대한 경우이다.

[Univariate Density]

  변수가 하나 존재할 때 표현하는 방법이다.

[Normal density]

 

[mean]

[variance]

[$p(x)~N(\mu,\sigma^2)$]

[multivariate Density]

  변수가 여러개 존재할 때, 행렬을 이용하여 나타내야 한다.

[Normal density]

[mean]

[covariance matrix]

[Statistical independence]

  $x_i$와 $x_j$가 statistically independent인 경우, $\sigma_{ij}=0이다.

[Transform]

  $p(x)~N(\mu,\sum)$인 경우, Transform된 $y=A^tx$라 하면, $p(y)~N(A^t\mu,A^t\sum A)$가 된다고 한다. 

  위 그림에서 우리가 얻고자 하는 것은 cluster의 모양이 spherical하게 만드는 것이 목적이 될 것이다. 이를 다차원으로 옮기면 hyperspherical이라고 말하며, 이는 $\sigma_{ij}=0$으로 만들어 주는 과정뿐만 아니라, 분산행렬이 단위행렬이 되도록 만들어주는 과정이될 것이다. 그에 해당하는 $A_w$는 다음과 같다. 

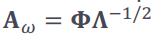
  위 식에서 $\phi$는 column이 $\sum$에 대한 orthogonal eigenvectors로 이루어진 행렬이고,

  $\Lambda$ eigenvalues로 이루어진 diagonal matrix이다.

  

https://twlab.tistory.com/54

[Linear Algebra] Lecture 25 대칭 행렬(Symmetric Matrix)과 스펙트럼 정리(Spectral Theorem)

  이렇게 나올 수 있는 배경에는 $\sigma_{ij}$=$\sigma_{ji}$인 대칭행렬이라는 점이 이용될 것이다.

  대칭행렬의 고유벡터들은 서로 수직이며, 방향 성분만을 나타내는 단위벡터로 만들 수 있을 것이다. 정규직교벡터, orthonormal vetor로 구성된 직교 행렬은 square matrix일 경우, $Q^TQ=I$에서 $Q^T=Q^{-1}$을 만족하게 된다. 

  또, eigen value, eigen vector는 조금 뒤에 설명하겠지만, $Ax=\lambda x$를 만족한다. 여기서 $\lambda$를 대각행렬로 만들어 $\Lambda$로 만들어주면, $A\Phi=\Lambda\Phi$를 만족한다. 위 두 부분을 이용하면 유도할 수 있을 것이다.

 

 

 

[Mahalanobis distance]

  cluster의 모양은 $\sum$에 의해 결정된다. loci of points는 등고선과 비슷하게 사용된다. 위에 빨간 선에 해당한다고 할 수 있고, 밀도가 같은 영역끼리 나누게 된다. 즉, $(x-\mu)^t\sum^{-1}(x-\mu)$가 일정한 곳에 해당한다. 이 거리를 Mahalanobis distance라 한다. 따라서 $\sigma$의 eigenvalue가 위 그림의 타원의 장축과 단축을 결정할 수 있게 되는 것이다. 이는 eigenvector축에 대한 분산이 클수록 멀리 떨어져 있음을 뜻하고, 분산이 작을수록 평균에 모여있음을 의미하게 되는데, 그에 따라 밀도가 달라지게 될 것이므로, 분산의 개념을 생각하면 $sigma$의 eigenvalue에 의해 결정된다는 것이 자연스럽게 유도될 수 있을 것이다.

 

[c.f. Eigenvectors]

 

(  https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors 참조 )

  Eigenvector를 잘 설명해주는 그림이다. 위 그림에서 파란색과 핑크색이 Eigenvectors이다.  

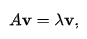
  위 식을 만족하는 벡터 v가 Eigenvectors이고, $\lambda$가 Eigenvalues이다. 또, 위 그림에도 알 수 있듯이 eigenvector들 끼리는 서로 orthogonal하다.

2.6 Discriminant Functions for the Normal Density

  위에서 discriminant function을 위와 같이 변형할 수 있었다. 이는 posterior probability로 부터 나온 식이므로, 최대가 되도록 하는 것이 목적이 될 것이다.

  normal distribution에서의 density function은 다음과 같았다.

  이를 discriminant function에 대입하면 다음과 같다.

[Case 1: $\sum_i = \sigma^2 I$]

  위에서 가장 간단한 케이스부터 살펴보자. 분산행렬의 모든 대각성분들이 $\sigma^2$으로 나타나고, 나머지 항들이 0이 된다. 이에 따라 모든 분산행렬이 hyperspherical cluster를 갖게 되고, i번째 class의 cluster는 $\mu_i$ mean vector에 중심을 갖게 된다. 또한, 다음과 같이 분산행렬에 대해 간단하게 구할 수 있다.

  이제 discriminant function을 구해보자. 위에서 $d/2ln{2pi}$가 포함된 항과, $1/2ln|\sum_i]$항은 i에 independent 하므로 다음과 같이 나타낼 수 있다.

  여기서, Euclidean norm을 사용하였는데, 다음과 같다. 이는 거리개념으로 생각해도 될 것 같다. norm은 norm 공간의 정의를 만족하는 원소이다. 조건을 보면 거리개념으로 생각할 수 있는 이유를 생각해볼 수 있을 것이다.

https://en.wikipedia.org/wiki/Norm_(mathematics)

  여기서 $x^tx$는 i와 관계없이 동일하므로 이 항을 제거하여 생각해도 각 $g_i(x)$항들의 대소관계가 어긋나지 않으므로 다음과 같이 나타낼 수 있다.

  $g_i(x)=g_j(x)$인 hyperplanes를 정해볼 것이다. 이는 two categois 상황에서 $\omega_i$와 $\omega_j$를 정하는 확률이 같은 경우이다.

  식 정리할 때 $\mu_j^t\mu_i = \mu_i^tmu_j$임을 이용해야 하고, 이는 좌항과 우항이 각각 스칼라 값이기 때문에 정리 가능하다. 나머지는 식 정리하는데 큰 어려움이 없었다.

  위에서 특징적으로 볼 수 있는 부분은 mean vector의 차에 수직인 평면을 나타낸다고 할 수 있다. 수직인 것은 변하지 않으므로 prior 값($P(\omega_i)$)에 따라 변하는 것은 hyperplane이 평행이동하는 것이다. 

  또한, prior값이 각각 0.5라고 한다면, 평균벡터 사이의 수직인 평면 중, 중점을 지나는 hyperplane이다. 

 

 

[Case 2: $\sum_i = \sum$]

  모든 클래스에 대해 $\sum$이 같은 경우이다. 특징적으로는 hyperellipsoidal clusters가 모두 같은 사이즈와 모양을 가지게 된다.

  이제 discriminant function을 구해보자. 위에서 $d/2ln{2pi}$가 포함된 항과, $1/2ln|\sum_i]$항은 i에 independent 하므로 다음과 같이 나타낼 수 있다.

  위 식을 전개할 때 $x^t\sum^{-1}x$ term은 i에 independent하므로 다음과 같이 쓸 수 있다.

 

   discriminant function이 마찬가지로 일차식인 것을 주의깊게 볼 수 있다. 위와 마찬가지로 $g_i(x)=g_j(x)$인 경우를 구하면 다음과 같다.

  여기서도 마찬가지로 일차식이기 때문에 hyperplane으로 $x_0$가 정해진다. 또한, $w^t(x-x_0)=0$을 만족해야 하기 때문에 w평면에 대해 수직인 성분을 나타낸다. prior에 따라 바뀌는 것은 hyperplane이 평행이동 한다는 점이다.

  [Case 3: $\sum_i = arbitrary$]

  이 케이스에서는 $d/2ln2\pi$만 i에 대해 independent 하다.

 

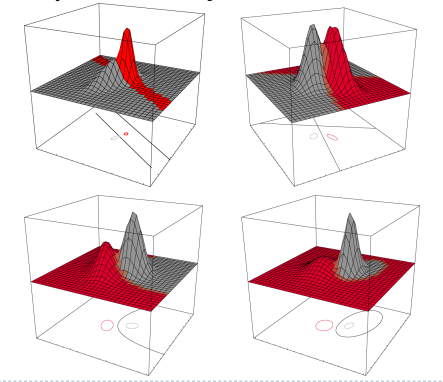
  여기서는 discriminant 함수가 2차식이므로, hyperplanes 형태가 아니라 hyperquadrics의 형태이다. 

---

Reference

• pattern classification by richard o. duda